Lack of Precision in Floating point numbers...

Binary Integer Numbers

Positives

Every number is represented using binary digits inside a computer. For example, 0 is 0, and 1 is 1. But after that every other number is represent using some combination of 0s or 1s.

2 => 10, 3 => 11, 4=100,...

Negatives

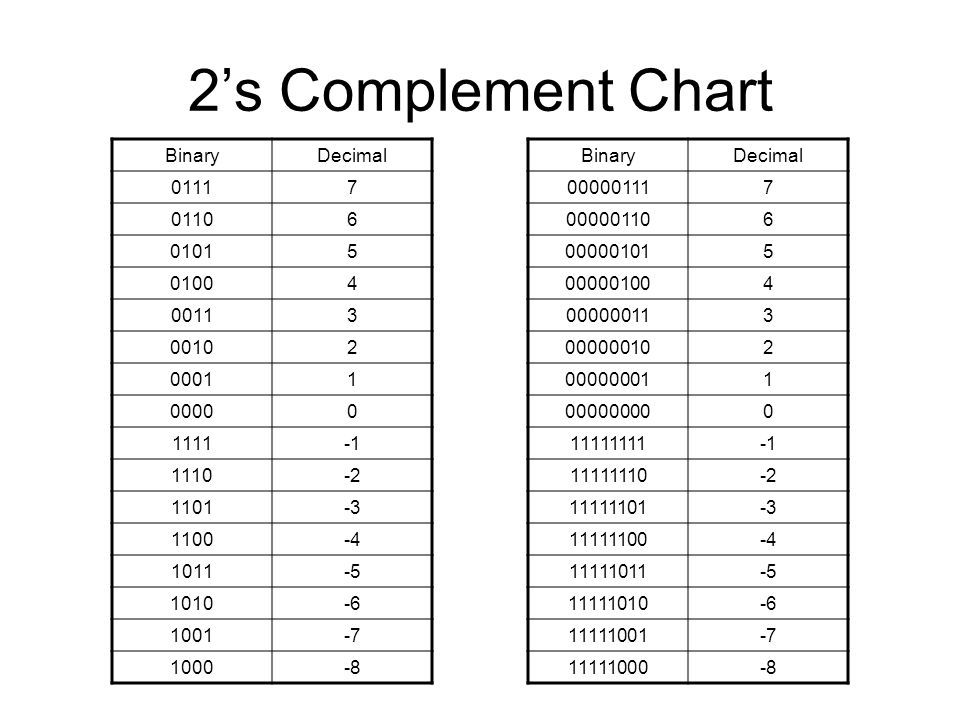
Even the numbers with negative signs are stored as binary, the only difference in storing them is that we first find out the 2's compliment of that number before storing or using it in any calculations. To calculate 2's compliment,

1. Flip all the bits to find the one's compliment.
2. Add 1 to the number to get a 2's compliment.

Floats / Fractions

In computers, a number with a decimal point somewhere in the middle of the digits is called a floating point number. IEEE 754  is the format for storing floating point numbers in most common languages, like C++, Java and python.

An IEEE 754 32 bit floating point number is stored in scientific notation,

$-1^{[s]}*2^{[exponent=8]}*1.[mantissa=23]$

and in this notion we use exponent to be a biased value, meaning that it has to be added to 127 before being used. So the number that is actually stored in the 32 bit format is like this(1+8+23=32 bits float),

$[s=1 bit][127-(exponent=8)][mantissa=23]$

this is called a single precision floating point number and there is correspondingly a double precision which is 64 bits long.

$-1^{[s]}x2^{[2048-(exponent=12)]}x1.[mantissa=52]$

In IEEE 754 standards there is no float that has an infinite precision, no format in which you specify the number you want to store and it gets stored as that value. There is always going to be a mismatch in those 2 values and higher the precision closer the stored value is going to be to the real value.

Because of all this precision requirements it is going to be very hard to store the exact values of a float. This can prove to be a big problem in data critical scenarios in finance, like stock markets, where all the calculation are done in floats.

IEEE 32 bit Floating Point numbers

Let's store a simple number, 1.2. What will shock you is that the number which is actually getting stored is 1.2000000476837158203125. This is not what you requested, you have got an error of about 4.76837158203125E-8! Believe it or not, this is how the currently things are being done under the hood.

Let's represent 1.2000000476837158203125 in binary,

sign bit=[0]

exponent of 2=[01111111]

exponents are 127 shifted, do 127 - exponent to get the real exponent of 2.

mantissa(.12)=[00110011001100110011010]

Clearly, the error in the mantissa part because , somehow in the process of calculating something is not right, let's look at it next.

Mantissa Calculation

Mantissa is calculated using negative powers of two,

$N = (0 or 1)2^{0} + (0 or 1)2^{-1} + (0 or 1)2^{-2} + ...$

Precision, here is defined as the number of terms we can use to define the original number N and if we had infinite series of all the negative powers of two, then, we could, in principle, store N exactly! Unfortunately that is not the case.

Changing the last bits of mantissa means that we are creating the smallest possible change in the system. This smallest change in the value of mantissa is called an Epsilon(=1.19e-07). Let us print a number represented by an epsilon down from our representation of 1.2, 1.19999992847442626953125, and one epsilon above, 1.20000016689300537109375.

Hence, the machine chose the closest representation for us and stored it as storing just 1.2 is not possible through the binary representation.

There is also the thing about the density of floats. As we have seen that, in 32 bits, we move in a unit of Epsilon, so not all the rational numbers are included. But, along with that there is an irregularity of distribution of these floating point numbers. There are much more representations in between 0 and 0.1 and in any other range of same length.

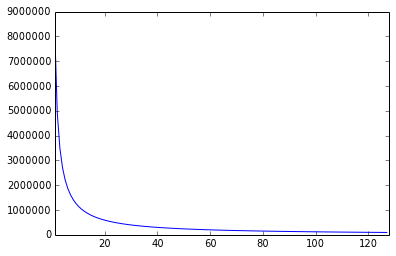
What this tells us is that we should keep our calculations normalized (between 0-1) or else the loss in precision will render all the calculations useless. The reason for this is the exponent bit, with every raising power of 2 the density gets halved.

For the case of 64 bits IEEE 754 floating point representations, the issues are the same just that it is better than the 32 bits counterpart just because of the increase of mantissa bits from 23 to 52.

Errors in performing Operations

The IEEE standard requires that the result of addition, subtraction, multiplication and division be exactly rounded. That is, the result must be computed exactly and then rounded to the nearest floating-point number. In order to facilitate just that, we need a few more bits along with our regular 32 bits and 64 bits just for the time we do the calculations and we store the result after rounding it off closer to an even number (rounding-even).

[s][exponent][mantissa][GUARD][ROUND][STICKY]

Guard bit and the Round bits are just an extra set of precision. Sticky bit is an OR to whatever that is shifted. The Guard and the Round bits decide whether the final result is rounded up or down before storing it in the standard representation.

In order to be able to perform any binary operation, the exponents of two floating point numbers are matched first. The mantissa is shifted for one of the numbers if the exponents do not match. Guard bit holds some of the bits that have overflowed out of the shifted mantissa.

The combination of the guard bit and the round bit decides the rounding. For more information and better explanation, please watch this amazing video on YouTube by John Farrier.

Conclusion

We have seen that it is impossible to represent all the rationals using the IEEE 754 floating point representation. Floating point number move in Epsilons and so, rounding occurs and the values get modified to the nearest value that can be represented using that many bits. This modification can be a problem and the calculations using these modified values are going to be even more erroneous.

Either use software math libraries which use some other representation of these numbers, either using integers because integers do not lose precision like floats do. Every programmer should know about these rounding and floating point issues to write better code.