Minimum Quantum Mechanics theory for Quantum Computing...
Building a virtual quantum computer-101!!
Mathematical basics of quantum mechanics to understand the working of a quantum computer...
Generally there are two kinds of physics which govern everything that we see around us, first is a point particle mechanics and the other is the wave mechanics. Quantum mechanics is nothing but a glorified and heavily tested wave theory which predicts the probabilities of an event rather than the events themselves.
Let's toss a coin. We know that if the coin is fair it is equally likely to land HEADS or TAILS. It is called a 50% probability of each event. According to quantum mechanics:
Until a measurement has been made, the system stays in all the possible configurations as it can be in, simultaneously!
Simultaneously being in the state of HEADS and TAILS is not easily imagined by the common public. It is only at the time of measurement the coin attains a single value of outcome, either HEADS or TAILS, never both, never neither.
The time when this was realized by the scientists, Albert Einstein was absolutely against this psychology of reality, saying that the 'God Does not play dice' . He said that because we are not measuring before the measurement, we don't know what is the state the system is in but it would be absurd to just say that it stays in the superposition of every possible outcome! He was proven wrong in 1964 by John Bell of Bell labs. More about Bell's Inequality on Wikipedia.
It just happens so that the world is lot more complex than we think and although we don't have a clear picture of what is looks like at the tiniest scales of quantum mechanics we still have the perfect working mathematical model of how it works and how to perform calculations out of this complexity. Because of this added complexity, quantum computers outperform classical computers in some aspects.
Complex Interlude
There is a little mathematical requisite in order to move forward learning quantum mechanics basics, Complex Number. So basically these are the number which include $i = \sqrt{-1}$ in their calculations. $$C = a + ib$$ where $a$ and $b$ are real numbers and has no complex part. The rule for doing all the calculations is this: $i^2=-1$, for ex, $$(a+ib)(c+id)= ac+iad+ibc+i^2bd$$ $$=> (ac-db) + i(ad+bc) $$
Concept #1: State
A state is represented by a vector in Hilbert Space, which describes the state that the system is in.
For the state of a coin toss,
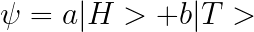
where if the coin is fair will have the value of 'a' and 'b' equal to,
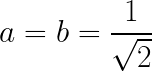
and the |H> is known as the state that the system is in the state HEADS. The constants 'a' and 'b' denote the complex amplitude( these are complex numbers) of being in the state |H> and |T>.
In quantum mechanics, the state vector is the only thing which can be known about any state. There is literally nothing else to be known about other than the state vector.
Concept #2: Probabilities
In order to calculate the probability of a particular state to be attained upon measurement, we square the amplitudes associated with that particular state! For example, if you want to calculate the probability of being in state |H>, you will have to square the constant associated with it, namely 'a'.
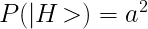
Concept #3: Bases of the state vector
So Whats a bases?
Since every state is a vector, we may define a set of bases vector for these states. Until now, we have been using the bases of $|H>$ and $|T>$ to represent HEADS and TAILS.
There can be multiple bases and we can transform our vector into a vector in any particular bases states
For real world quantum computing applications, the bases of electron spins is used, namely
So how do we switch bases?
The answer is Superposition. There is a kind of orthogonality which is there in the bases vectors, which means that the dot product of two bases vectors is zero if they are orthogonal. $$< RIGHT | LEFT > =0$$ The ket $RIGHT$ vector is in the mixture or superposition of states $UP$ and $DOWN$ $$ |RIGHT> = 1/\sqrt{2}(|UP>+|DOWN>)$$ $$ |LEFT> = 1/\sqrt{2}(|UP>-|DOWN>)$$ Since $RIGHT$ has some components of both the bases, $$ < RIGHT | UP > \neq 0 $$ or $$ < RIGHT | DOWN > \neq 0$$
We can replace $ |RIGHT>$ with $ 1/\sqrt{2}(|UP>+|DOWN>)$ and $ |LEFT> $ with $1/\sqrt{2}(|UP>-|DOWN>)$ and that concludes the transformation in the state vector equation!
Concept #4: Operators
An operator is simply a matrix like object which acts on a state vector to transform it into another vector. All operations in quantum mechanics are linear, something to keep in mind.
First we write our bases vectors in column matrix notation,
$$|UP> = \begin{pmatrix} 1\\\ 0 \end{pmatrix}$$
$$|DOWN> = \begin{pmatrix} 0\\\ 1 \end{pmatrix}$$
Let's take an operator $M$ which does nothing, it is equal to $I$ (identity matrix) just to see how the calculation goes. We write,
$$M =\begin{pmatrix}1 \:\:\: 0 \\0 \:\:\: 1\\ \end{pmatrix}$$
Operator is applied using the same old matrix multiplication, $$M|A\!> = |A\!>$$ $$\begin{pmatrix}1 \:\:\: 0 \\0 \:\:\: 1\\ \end{pmatrix}\begin{pmatrix}1 \\0 \\ \end{pmatrix}=\begin{pmatrix}1 \\0 \\ \end{pmatrix}$$
A Not(X) operator flips a state vector $$M|A\!> = |B\!>$$ $$\begin{pmatrix}0 \:\:\: 1 \\1 \:\:\: 0\\ \end{pmatrix}\begin{pmatrix}1 \\0 \\ \end{pmatrix}=\begin{pmatrix}0 \\1 \\ \end{pmatrix}$$ All the numeric entries in the matrices and vectors are complex in general. Remember, $ |RIGHT>$ is $ 1/\sqrt{2}(|UP>+|DOWN>)$. This state is a superposition of UP and DOWN states. Let's write the equation in matrix notations and calculate |RIGHT>. $$ |RIGHT>= 1/\sqrt{2}(\begin{pmatrix} 1\\\ 0 \end{pmatrix}+\begin{pmatrix} 0\\\ 1 \end{pmatrix})$$ $$ |RIGHT>= 1/\sqrt{2}\begin{pmatrix} 1\\\ 1 \end{pmatrix}$$ $$ |RIGHT>= \begin{pmatrix} 1/\sqrt{2}\\\ 1/\sqrt{2} \end{pmatrix}$$ We say that |RIGHT> is the superposition of |UP> and |DOWN>. There is a matrix, which when applied to |UP> or |DOWN> create a superposition of both the states in the resultant vector. It is called as the Hadamard Operator, and, is equal to,
$$H =1/\sqrt{2}\begin{pmatrix}1 \:\:\:\:\: 1 \\1 \:\:\: -1\\ \end{pmatrix}$$
Concept #5: Eigenvalues
These operators change the state vector into another vector. For some operators there are some special vectors which do not change their direction and simply get scaled up or squished down by a scalar. These vectors are known as Eigenvectors of that matrix. The amount of scaling is denoted by a complex constant known as Eigenvalue.
$\lambda $ is the eigenvalue and $|\lambda>$ is the eigenvector, $$M|\lambda> = \lambda |\lambda >$$ For Identity operator, 1 is the only eigenvlaue and every vector is an eigenvector! $$\begin{pmatrix}1 \:\:\: 0 \\0 \:\:\: 1\\ \end{pmatrix}\begin{pmatrix}1 \\0 \\ \end{pmatrix}=1\begin{pmatrix}1 \\0 \\ \end{pmatrix}$$ For Swap(or X or NOT) operator, 1 is the eigenvlaue and $\begin{pmatrix}1/\sqrt{2} \\1/\sqrt{2} \\ \end{pmatrix}$ is an eigenvector! $$\begin{pmatrix}0 \:\:\: 1 \\1 \:\:\: 0\\ \end{pmatrix}\begin{pmatrix}1/\sqrt{2} \\1/\sqrt{2} \\ \end{pmatrix}=1\begin{pmatrix}1/\sqrt{2} \\1/\sqrt{2} \\ \end{pmatrix}$$
Hermitian Operators!
These are the most useful ones as I have understood operators. These operators are related to the Observables in the real world, for example, position and momentum. Hermitian Operators are those operators which are their own Hermitian-Conjugates. Hermitian conjugation of an operator means taking a transpose and then complex conjugating all the member elements.
$$A^\dagger=[A^T]^*$$
The Hermitian matrices have a property that they only have real eigenvalues and all the eigenvectors that exist form a set of orthogonal bases.
The most important property is that the eigenvalue of a Hermitian Operator are real and are the values which are observed in the real world experiments. That is why, they have names like position and momentum. In the case of an electron, we are going to use a spin(quantum spin) operator which gives us the amount of spin in a particular axis.
Note: Measurements have a very different meaning in Quantum Mechanics. Applying operator does not mean we have done a measurement but just that we have transformed the state vector. In order to perform a measurement we need to include the apparatus state vector into the state vector. This would involve some tensor product that we will see later
There are 3 spin operators, one for each axis, x,y and z. These are named after Wolfgang Pauli and are called Pauli Matrices.

This states that in order to be able to measure spin along X axis, you would use the $\sigma_{x}$ and the corresponding eigenvalue gives you the answer you are looking for.
The spin state is represented on a Bloch Sphere by an arrow.
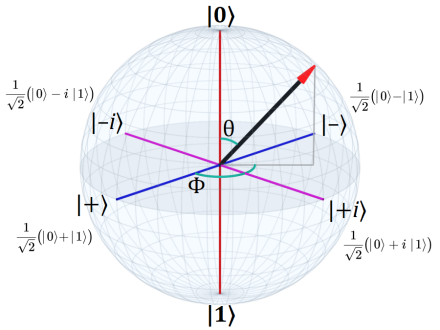
Every operator applied rotates this vector somewhere on the bloch sphere. More about the Bloch Sphere on Wikipedia.
Concept #6: Time & Hamiltonian, story of a Unitary....
Up until now, we have seen what a state is and how operator act upon it to transform it into something else, but we have not discussed how the system evolves with time. For that we need some Unitary Operators.
Unitary Operators
The operators which upon hermitian conjugation, produces its own inverse are called unitary operators.
$$U(t)U^\dagger(t) = I $$
They are important in quantum mechanics because all time evolution operators are unitary.
$$|\phi(t)> = U(t)|\phi(0)> $$
Determinism has not left the realm of physics even in the case of quantum mechanics. State evolution is deterministic when transformation is induces using unitary operators. Unitary operators conserve distinctions. if two states start orthogonal, they are going to maintain this distinction throughout as both transforms under the same operator.
Deriving Time-Dependent Schrodinger Equation!
Let's assume that an operator $|U(t)>$ produces an infinitesimal change.
$$|U(t=\epsilon)\!> = I-i \epsilon H $$
Taking hermitian conjugate, we get
$$|U^ \dagger (t=\epsilon)\!> = I+i \epsilon H^ \dagger $$
Now, Since $U(t)U^\dagger(t) = I $,
$$(I-i \epsilon H)(I+i \epsilon H^ \dagger)=I$$
Solving this leads to,
$$H^\dagger = H$$
Therefore, H is a hermitian operator, with a full set of eigenvector bases. But, H is also unitary, therefore at $t= \epsilon $,
$$| \psi (t= \epsilon )\!> = | \psi (0)>-i \epsilon H| \psi (0)> $$
Rearranging the terms,
$$\frac{| \psi ( t=\epsilon )\!> - | \psi ( 0 )\!>}{\epsilon}=-i \epsilon H| \psi (0)\!>$$
Those of us who are familiar with calculus can realize that this is equal to:
$$\frac{ \partial | \psi\!>}{ \partial t} = -i \epsilon H| \psi (0)\!>$$
phew....That is the so called Schrodinger equation!
H is called the Hamiltonian, it represents energy of the system. To think about, the rate at which the state function changes corresponds to the energy of the system. This change in state function is responsible for the apparent kinetic energy in the system.
Tensor Interlude
To understand entanglement, first we have to understand what a tensor product is because it is what we use to create entanglement between two state vectors and make a single state vector as an output. It is a type of matrix product which is actually simpler than the conventional matrix product.
Tensor Product of Matrices!
$$\begin{pmatrix}
a & b\\
c & d
\end{pmatrix}
\bigotimes
\begin{pmatrix}
w & x\\
y & z
\end{pmatrix}=\begin{pmatrix}
a\begin{pmatrix}
w & x\\
y & z
\end{pmatrix} & b\begin{pmatrix}
w & x\\
y & z
\end{pmatrix}\\
c\begin{pmatrix}
w & x\\
y & z
\end{pmatrix} & d\begin{pmatrix}
w & x\\
y & z
\end{pmatrix}
\end{pmatrix}$$
$$=>\begin{pmatrix}aw & ax & bw & bx \\ ay & az & by & bz \\ cw & cx & dw & dx \\ cy & cz & dy & dz \\ \end{pmatrix}$$
Can even multiply 2 column vectors!
$$\begin{pmatrix}
a \\
b
\end{pmatrix}
\bigotimes
\begin{pmatrix}
c \\
d
\end{pmatrix}=\begin{pmatrix}
ac \\
ad \\
bc \\
bd \\
\end{pmatrix}$$
Concept #7: Entanglement
Entanglement is an intrinsic property of quantum mechanical systems. It has no classical counterpart. That was why people like Albert Einstein were trying to prove that quantum mechanics is absurd but instead he kept on discovering mind boggling phenomena in this quest.
Let's consider an experiment. Alice and Bob, from another galaxies, put 2 balls in a bag, one red and one black. Without looking at the balls, each pick one and head of their respective galaxies. Now we know that the these colored balls are separate entities. If Alice, after reaching it's galaxy looks at the color of the ball she got, she immediately knows which color ball has Bob picked because of the precondition that there were only these 2 balls initially. Nothing weird in this scenario.
Now, the quantum mechanical entanglement states that, up until the point any one of them made a measurement of the color of their ball, both of the balls stay in state of being one or another and only after measurement it chooses a final color. And when one looks at their ball, magically the other ball also loses the state of entanglement and decides to stay with a certain color.
The problem with this is in trying to imagine what the reality looks like when it is entangled. Let's take a system with 2 electron, each with a spin in |UP> and |DOWN> bases. When these spin states are entangled they form a new state in which it is impossible to tell what a spin state is of a single particle. The only thing that can be said is about the system of both of these states.
$$|Alice> = \begin{pmatrix} a\\\ b \end{pmatrix}$$
$$|Bob> = \begin{pmatrix} c\\\ d \end{pmatrix}$$
$$|Entangled> = |Alice> \bigotimes |Bob>$$
$$|Entangled> = \begin{pmatrix}
a \\
b
\end{pmatrix}
\bigotimes
\begin{pmatrix}
c \\
d
\end{pmatrix}=\begin{pmatrix}
ac \\
ad \\
bc \\
bd \\
\end{pmatrix} $$
Concept #8: Measurement
Expectation Value of an operator!
Expectation value of L(<L>) is in general defined as,
$$<L>=\sum_{i}\lambda_{i}P(\lambda _{i})$$
In order to derive an expression we do the following calcualtions.
Let's expand our State vector in terms of its bases vector $\lambda_{i}$
$$|A\! > \; = \sum_{i}\alpha _{i}|\lambda _{i}\! >$$
Applying an operator L (which happen to have the same bases as eigenvectors) to the state above,
$$L|A\! > \; = \sum_{i}\alpha _{i}L|\lambda _{i}\! >$$
$$=>L|A > \; = \sum_{i} \alpha_{i}\lambda_{i}|\lambda _{i}\! >$$
Inner Product with the same state vector gives,
$$<A|L|A > \; = \sum_{i} (\alpha_{i}*\alpha_{i})\lambda_{i}=\sum_{i}\lambda_{i}P(\lambda _{i})$$
The term $(\alpha_{i}*\alpha_{i})$ is the probability and this equation gives us the expected value of L!
$$<L>=<A|L|A >$$
The expected value of an operator is closely related to the outcome of an actual measurement.
Commutators
To Commute operator A with another operator B, we write $$[AB]=(AB - BA)$$This produces a new operator to work with: $[A,B]$, called the commutator of A and B.
The condition for two observables to be simultaneously measurable is that they commute, that is their commutator, $[A,B]$, is equal to 0. If this is not the case then the wave function will end up in an ambiguous state after being applied with both the operators in any order. This is the case with the spin operators.
$$[\sigma_{x},\sigma_{y}]=2i\sigma_{z}$$
$$[\sigma_{z},\sigma_{x}]=2i\sigma_{y}$$
$$[\sigma_{y},\sigma_{z}]=2i\sigma_{x}$$
That is why, we can never measure spin along 2 different axes. End result is doomed to be uncertain.
Conservation Laws: An expected value of an operator depends on how it commutes with the Hamiltonian:H operator,
$$[L,H]$$
If the commutation results in $0$ then the operator has a conserved expected value, it won't change.
We can quickly realize that $H$ always commutes with $H$, since, $HH-HH=0$ always, stating that the quantity measured by the H operator, namely Energy, is conserved.
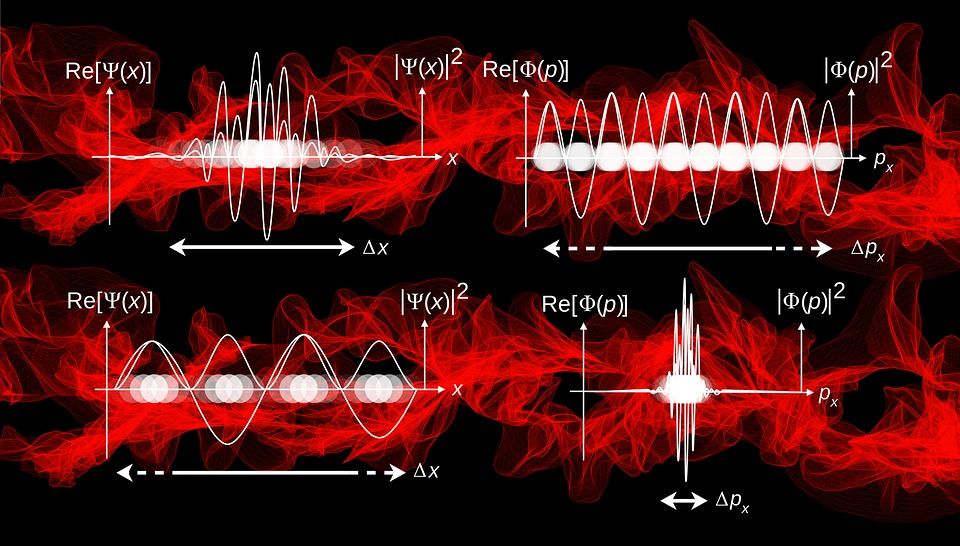
General Principle of Uncertainty!
Finally, we have made to the golden rule of quantum mechanics, Heisenberg's Uncertainty Principle. As you would have guess by now how we are going to get uncertainty in the system, for those who haven't, its Commutators. The general rule states that for two operators A and B, the amount of uncertainty you get is equal to,
$$\Delta A\Delta B = \frac{1}{2}<\psi|[A,B]|\psi>$$
If we consider position($X$) and momentum($P$), and try to commute them, we get,
$$[X,P]=i\hbar$$
$$\Delta X\Delta P = \frac{1}{2}<\psi|i\hbar|\psi>$$
$$\Delta X\Delta P = \frac{1}{2}i\hbar$$
Since, the result is not 0, it is impossible(theoretically and practically) to ever measure the real position and momentum simultaneously.
The Collapse: Measuring the observables
Measuring an observable of an operator $L$ over a state $|A>$ will give unpredictable result the the state $|A>$ is not in any eigenvector state of that operator $L$.
If the state was already an eigenvector, then the corresponding eigenvalue is measured.
Although, it is not necessary that the state is an eigenvector. In that case an unpredictable result will come forth. After the experiment the system ends up in an eigenvector($\lambda_{i}$) of $L$. Any subsequent operation will result in the same eigenvector and eigenvalue.
This is called the Quantum Mechanics collapse of the Wave function.